PID Controller using modern Microcontrollers
NOTE: This article/blog is Copyright TronicsZone. It cannot be reproduced without prior written approval.
Introduction
In industrial automation and control, PID has become the modern reliable workhorse. The applications of PID in industries ranges across regulating the flow, temperature, pressure, level, and many other industrial process variables. Without a PID controller, manual control of industrial process variables can become a tedious process. PID controller can be implemented using both digital and analog electronic circuit design. With the advent of digitization, it becomes essential to understand the implementation of PID with embedded systems. Modern Microcontrollers are powerful enough to implement a PID algorithm efficiently due to the processing capabilities and myriad of on-chip peripherals on them (like ADC, DAC, DMA etc.). This article discusses the working of PID and its implementation using a popular Arduino based microcontroller.
What is a PID?
PID is the abbreviation for proportional, integral and derivative. PID is a feedback control system. For example, let us consider an industrial process requires to control the temperature of the furnace. A sensor placed in the furnace provides us with the actual temperature. This sensor output is compared with the reference value that we have provided to the controller. The difference in these two values is the error. Based on the error value temperature inside the furnace is adjusted to obtain the required temperature. This is an example of a closed-loop system.
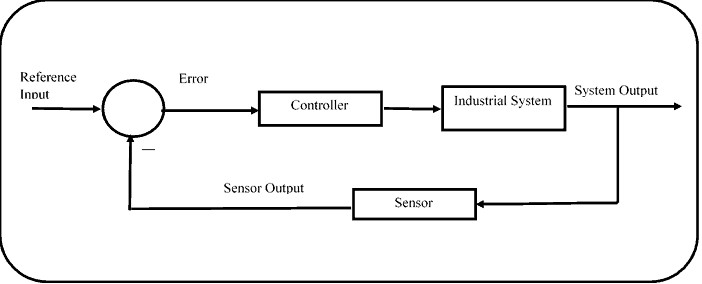
Working of a PID
In an industrial setup, the PID will act both electronically and mechanically. Consider an example of a dryer running to remove moisture in a washing machine. In a simple open-loop system, the dryer runs based on a pre-set timer and stops without making sure that the moisture is removed from the cloth. Now, in a closed-loop system with a PID controller, an error is generated when there is moisture in the cloth. This moisture is detected by a moisture sensor placed inside the system. The dryer runs till this error becomes zero. This closed-loop system automates the drying process and makes sure that the cloth is dry.
Proportional controller
As stated above, PID stands for proportional, integral, derivative. PID controller is one of the most commonly used and universally accepted controller. The term P is proportional value and it is proportional to the actual value of the error. This mode changes the controller output in proportion to the error from the feedback. As the error increases, the control action increases proportionally. In case of negative error reverse action is also possible in the proportional controller. Considering e(t) as the input error signal and u(t) as the controller output, The equation for the proportional controller device is given by
u(t) ∝ e(t)
u(t) = kp * e(t)
Where, kp is the proportional gain factor or the proportional controller gain. The response speed of the proportional controller is decided by the proportional controller gain value. Higher the value more fast is the response. Critical value of kp has to be selected since very fast response can lead to oscillation and it shall make the system unstable.
Proportional Integral (PI) controller
The main issue with using a proportional controller alone is that it introduces steady state error. Steady-state error is minimized by taking integral of the error. The Integral controller removes the offset steady state and bring back the steady state error to zero. The integral of the error is added with the proportional controller output. The equation is given by
u(t) ∝ (e(t) + ∫ e(t) dt)
u(t) = kp *e(t) + ki ∫ e(t) dt
Where ki is the integral gain constant. Similar to proportional gain constant, higher ki results in faster response and lower value results in slow response to change in input signal.
Proportional Integral derivative (PID) controller
The derivative part of the controller deals with the rate of change of the error. The integral reads the history of the error, while the derivative helps in predicting its change. With this prediction the differential controller responds fast enough to prevent the output from overshooting or undershooting the set point. The equation for the PID controller as a whole is given by
u(t) ∝ (e(t) + ∫ e(t) dt + de(t)/dt)
u(t) = kp *e(t) + ki ∫ e(t) dt + kd * de(t)/dt
Where Kd is the derivative gain constant. To sum up the action on the PID controller is that the proportional term optimizes the rise time the integral term eradicates the steady state error and the derivative term minimizes the overshoots and ringing.
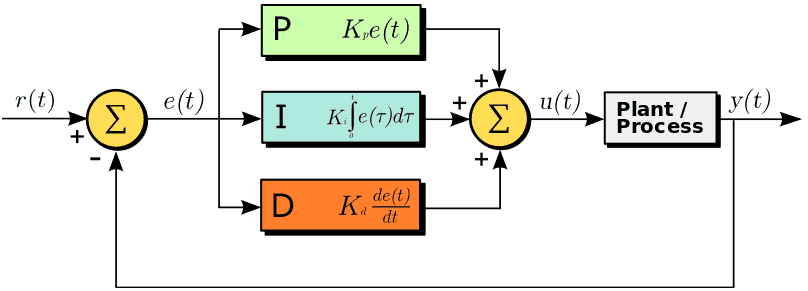
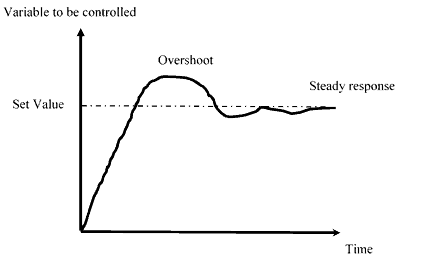
Output of a PID Device
The PID provides a steady and quick response to the variation in the input error signal. The following graph illustrates the steady response of the PID controller around the set value. The variable under control shall be temperature or pressure or any such industrial parameters.
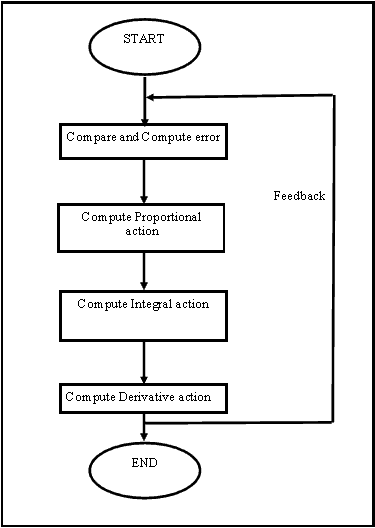
Implementation of PID with Arduino
The above equations are in analog domain since the sensor error signal output will be analog in nature. To implement in modern microcontrollers like the Arduino, the PID has to be implemented digitally. The PID equation can be written digitally as
u(n) = kp *e(n) + ki ∑ e(n)T + kd *( e(n)-e(n-1)/T)
Where T is the sampling time or a fixed time interval. The proportional term is obtained by multiplying the gain with the discrete error signal. The integral term is obtained by sigma summation and the derivative term is computed as the difference between the current error and the previous error.
The error signal is treated as discrete time input and the output is computed accordingly. Programs are utilized to realize the PID function in an Arduino processor. PID Library is available for calling as open source for Arduino. The programmer has to specify the kd, ki, kp and set point values alone. The flowchart for the algorithm is as follows
Applications of PID controllers
PID controllers find a wide range of applications such as Furnace Temperature Control, Neutralization pH Control in a chemical process, Designing of MPPT (Maximum power point tracking) charge controller for solar PV, Power electronics converter, and many more. The reliability and stability of the PID controllers make it the most sought after controller in the industry,
Conclusion
Thus the PID Controller provides a steady control response to an industrial process by computing the error response combining of all the present errors, past errors, and estimation of future errors. Even the simple Arduino is capable of implementing a PID algorithm in modern days. PID controllers are indispensable in modern process control systems and industrial automation & is a tool which is commonly used by us at TronicsZone while designing control systems.
NOTE: This article/blog is Copyright TronicsZone. It cannot be reproduced without prior written approval.

 TronicsZone
TronicsZone TronicsZone
TronicsZone